There’s one more thing we need to review before we step back and discuss why this simple system is so prevalent, and that’s the potential energy of the spring. As the block slides back and forth, it’s constantly speeding up or slowing down, and so its kinetic energy $\frac{1}{2} m v^2$ is changing. Its total energy, though, kinetic plus potential, is a constant, where the potential energy is given by $U = \frac{1}{2}k x^2$. We can check that by taking the rate of change of the total energy:
$$ \frac{\mathrm{d} }{\mathrm{d} t } \left\{ \frac{1}{2} m \left(\frac{\mathrm{d} x }{\mathrm{d} t } \right)^2+ \frac{1}{2} k x(t)^2 \right\} = m \frac{\mathrm{d} x}{\mathrm{d} t } \frac{\mathrm{d}^2x }{\mathrm{d} t^2 } + k x \frac{\mathrm{d} x}{\mathrm{d} t }. $$
We therefore get
$$ \frac{\mathrm{d}E }{\mathrm{d} t } = \frac{\mathrm{d} x}{\mathrm{d} t } \left( m \frac{\mathrm{d}^2 x }{\mathrm{d} t^2 }+ kx \right), $$
but the thing in parentheses vanishes by $F = ma$! Therefore, the total energy is indeed a constant.
Notice that the force $F = -kx$ is related to the potential energy $U = \frac{1}{2} k x^2$ by
$$ F = - \frac{\mathrm{d} U}{\mathrm{d} x }. $$
In other words, the force is equal to minus the slope of the potential energy curve. That’s the general relationship between force and potential energy. Notice that it means that in equilibrium, i.e. where the force is equal to zero, the slope of the potential must vanish.
In fact, you can think about the potential energy curve as if it were a frictionless hill with a particle sliding along it—in the case of the harmonic oscillator, the hill is a parabola $U \propto x^2.$ The equilibrium point is at the bottom of this well; if you set a particle at rest there at $x = 0$, it will happily sit there forever. If you set the particle down away from the equilibrium, however, it will rock back and forth about the bottom of the well, in the same way that the block oscillates back and forth around its equilibrium position. You can see these two corresponding motions side-by-side in the above animation.
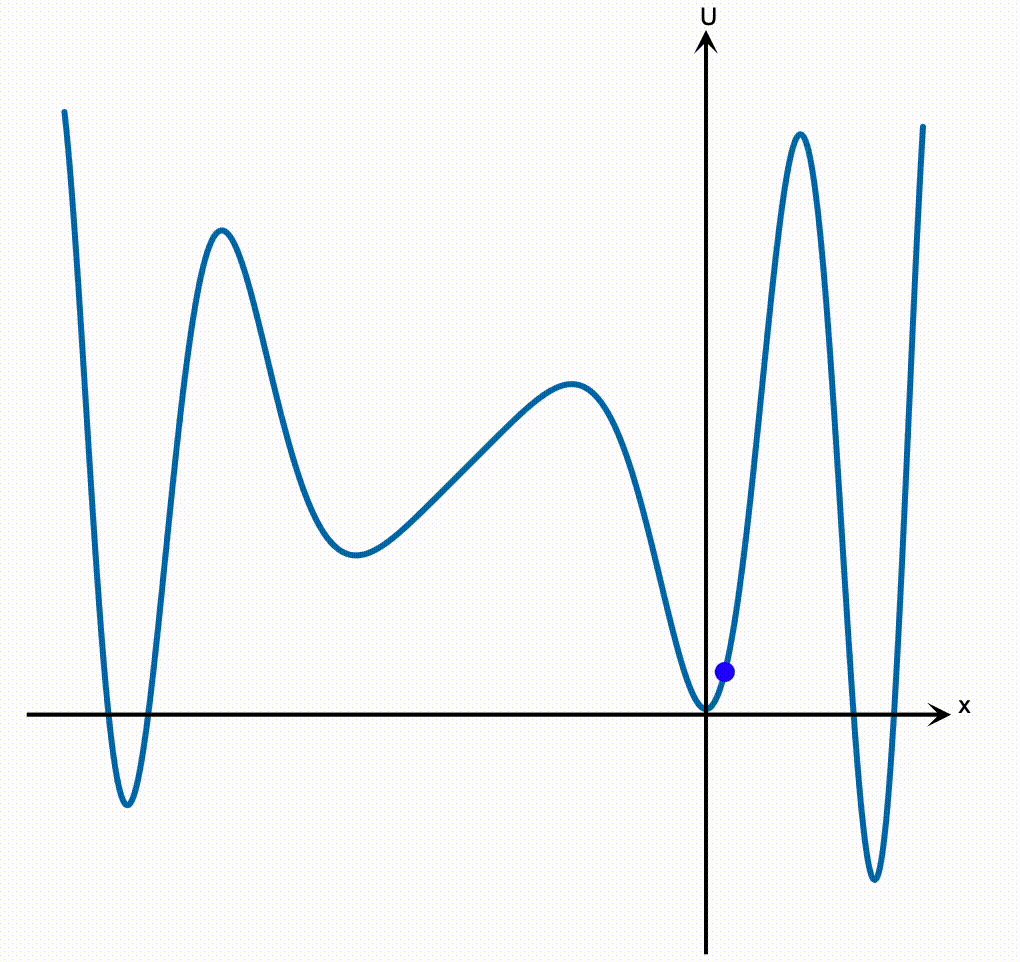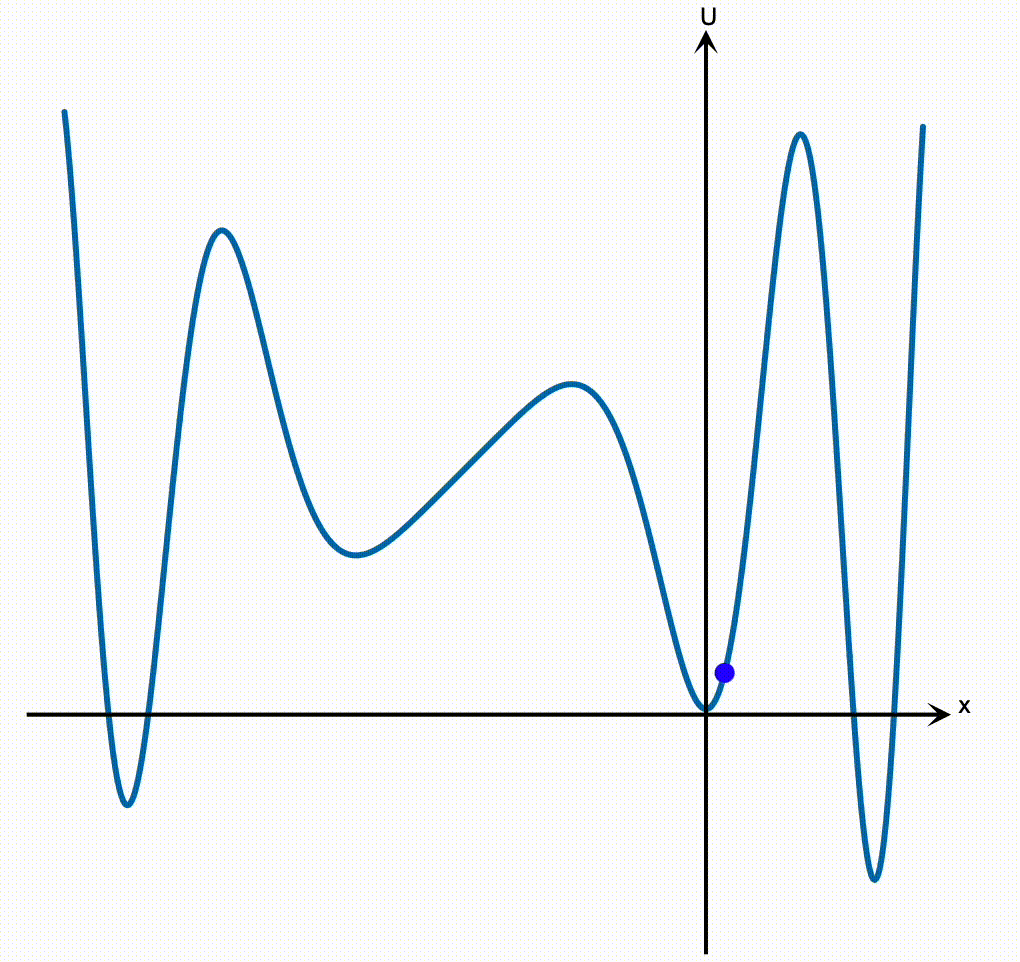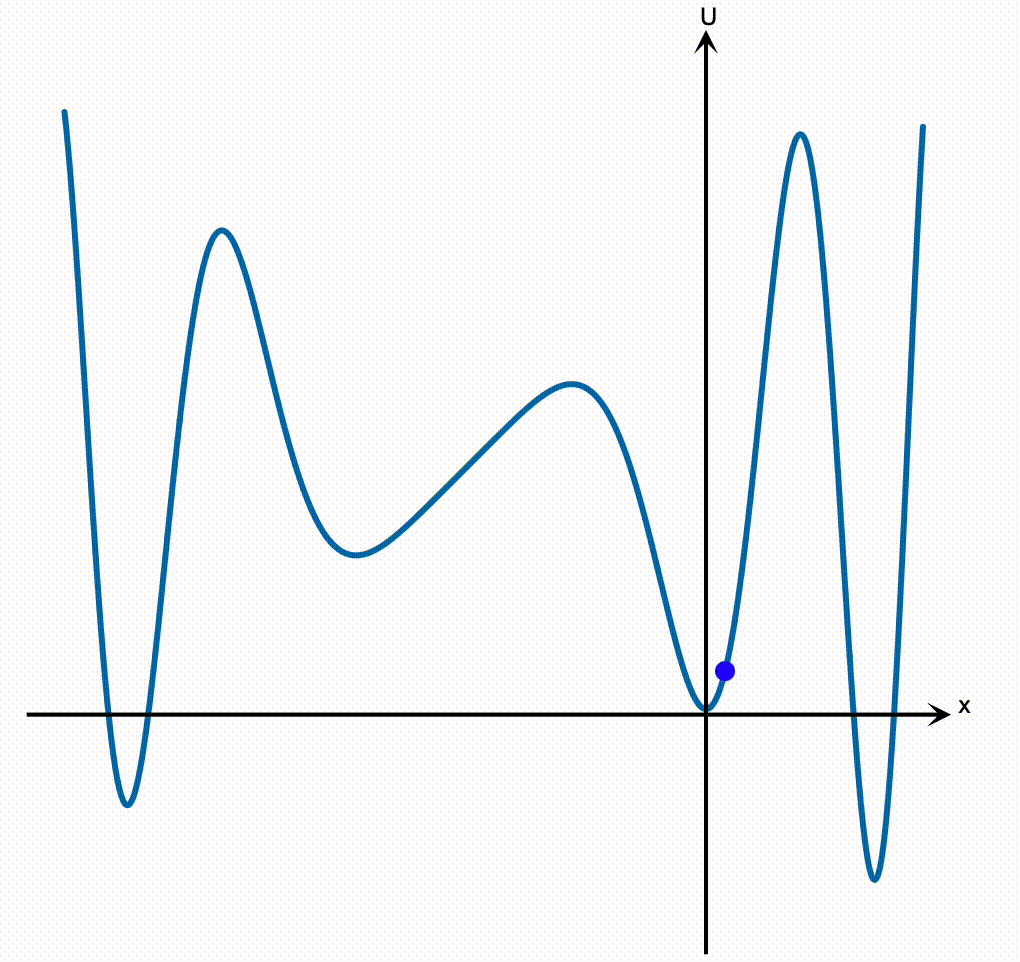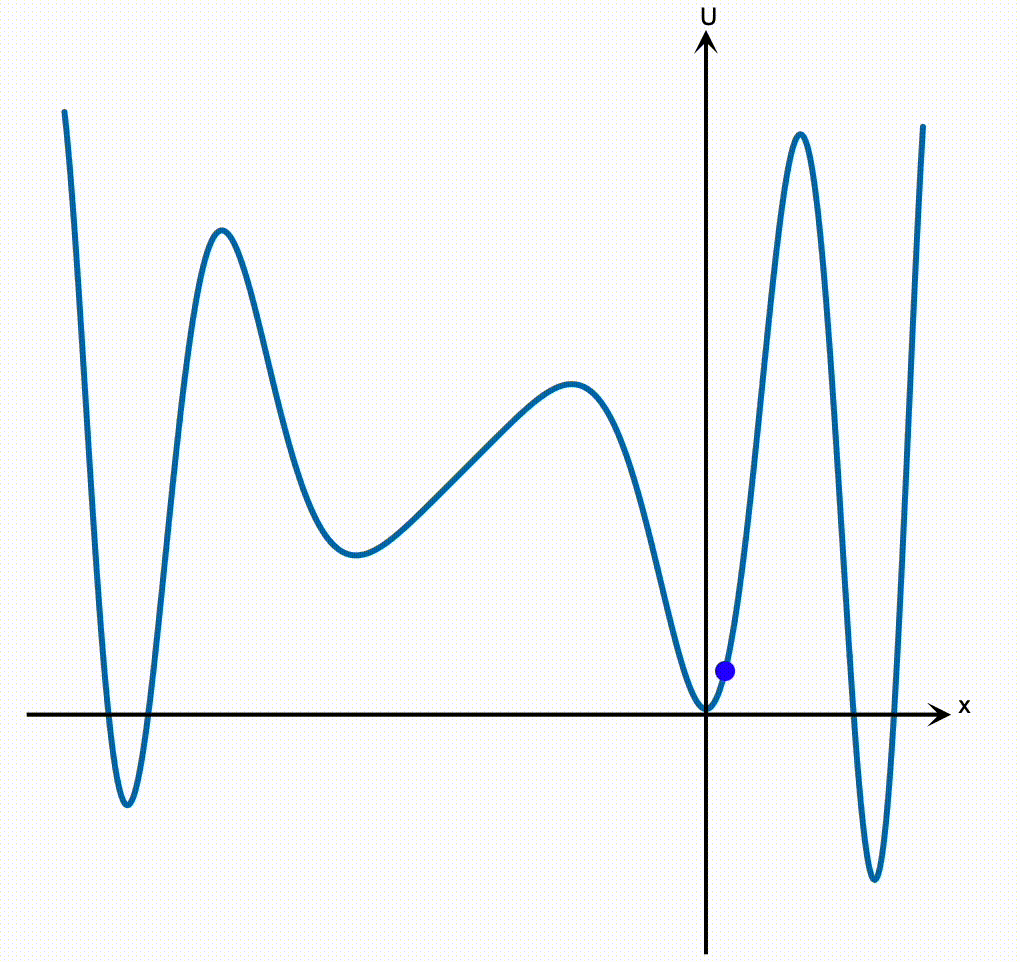
Thinking about the potential energy curve as a hill is a very powerful way of quickly developing your intuition for how a particle in a general potential will behave, without ever doing the hard work of trying to solve the $F = ma$ equation. In an earlier lesson, I told you about how we can apply that strategy to learn a ton about otherwise hard physics problems just by sketching a picture of the potential. Even with a very complicated potential, where we have no hope of writing down a simple solution for the trajectory, we can still qualitatively understand what the particle will do by picturing the potential like a hill.

Which brings us to the reason why the harmonic oscillator is so incredibly important and far-reaching. Consider a particle moving in any potential $U(x)$, like the random example above. We would like to once again solve the $F = ma$ equation,
$$ m \frac{\mathrm{d}^2x }{\mathrm{d} t^2 } = - \frac{\mathrm{d} U }{\mathrm{d} x }, $$
to determine the trajectory $x(t)$. But outside of a handful of potential energy functions described in textbook examples, finding a simple solution to this equation for a complicated potential like this will be a hopeless task.
So how can we make progress? The first thing you should do when someone hands you a potential energy curve is to identify its stable equilibrium points. An equilibrium is again a point where the force on the particle vanishes, and so the slope of the potential will be zero there. A stable equilibrium point is one that’s at the bottom of a well, as opposed to the top of a hill.
We can of course write down the exact solution to the $F = ma$ equation for a particle that’s set down at rest at an equilibrium point $x_\mathrm{eq}$: the force vanishes, and so the particle will just happily sit there forever!
$$ x(t) = x_\mathrm{eq}. $$
On the other hand, if you give the particle at a stable equilibrium a little tap, it will oscillate back and forth around the bottom of the potential, just like the block on a spring oscillates around the bottom of its parabolic well.
You’ll see this behavior all the time in your daily life if you pay attention. When you rock gently in a chair you’re oscillating around a stable equilibrium. When you drop an ice cube in a glass of water it bobs up and down around its equilibrium height. Your coat hanging on the hook is swaying slightly around its equilibrium axis. And the basic reason is that when you’re nearby a stable equilibrium point of almost any potential, the bottom of the hill looks just like the parabola of the simple harmonic oscillator.
And this isn’t some rough, qualitative analogy—we can make it mathematically precise.
See also:
If you encounter any errors on this page, please let me know at feedback@PhysicsWithElliot.com.