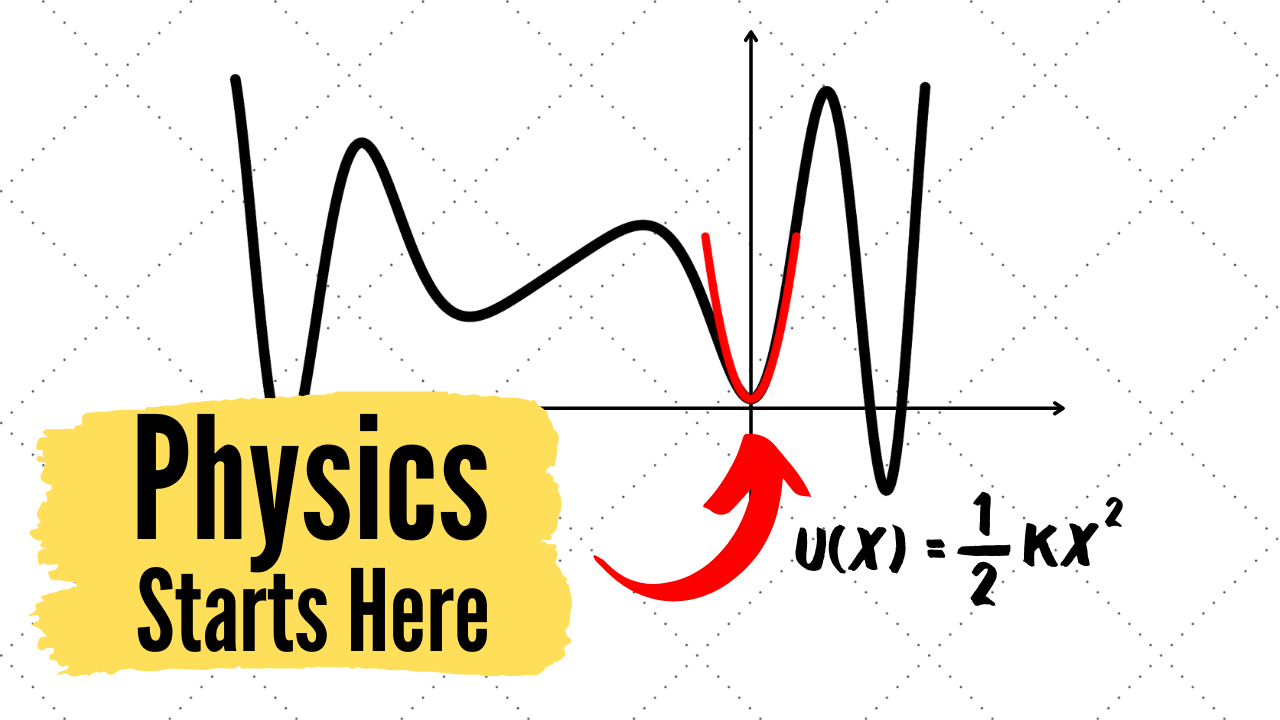
Expanding Around Equilibrium
Instructions: Any potential $U(x)$ can be expanded in powers of $x$ around a stable equilibrium point, like $x = 0$ in this example. Drag the slider to control the number of powers $n$ to include in the expansion, and see how well the red approximation matches the blue potential. For $n = 2$, the series expansion is a parabola, $U(x) \propto x^2$, and it does a good job approximating the potential near that equilibrium point. Recall that the quadratic potential $U(x) = \frac{1}{2} k x^2$ describes an oscillating block attached to a spring. Therefore, if a particle in this potential, or almost any other, is tapped slightly away from a stable equilibrium point, it will oscillate back and forth around the equilibrium just like a mass on a spring.
In a general potential, finding the exact solution to the equation of motion $m \frac{\mathrm{d}^2 x }{\mathrm{d} t^2 } = - \frac{\mathrm{d} U}{\mathrm{d} x }$ will be impossible. But using the quadratic expansion we can almost always write down the solution for a particle that doesn't stray too far from a stable equilibrium point: it's just a sum of sines and cosines. This is why the simple harmonic oscillator is such an important system: it describes the physics of almost every system near its equilibrium points.
Of course, if the particle has enough energy to move farther away from the equilibrium, the harmonic oscillator approximation won't be accurate anymore, as you can see by comparing the red approximation and the exact blue potential for $n = 2$. We can get a better approximation in a wider range by including more and more terms in the expansion, but these additions make even the approximated equation of motion difficult to solve once again.
If you encounter any bugs in this animation, please let me know at feedback@PhysicsWithElliot.com.